A short test on the code efficiency of CUDA and thrust

Introduction

Numerical simulations are always pretty time consuming jobs. Most of these jobs take lots of hours to complete, even though multi-core CPUs are commonly used. Before I can afford a cluster, how to dramatically improve the calculation efficiency on my desktop computers to save computational effort became a critical problem I am facing and dreaming to achieve.

NVIDIA CUDA seems more and more popular and potential to solve the present problem with the power released from GPU. CUDA framework provides a modified C language and with its help my C programming experiences can be re-used to implement numerical algorithms by utilising a GPU. Whilst thrust is a C++ template library for CUDA. thrust is aimed at improving developers' development productivity; however, the code execution efficiency is also of high priority for a numerical job. Someone stated that code execution efficiency could be lost to some extent due to the extra cost from using the library thrust. To judge this precisely, I did a series of basic tests in order to explore the truth. Basically, that is the purpose of this article.

My personal computer is a Intel Q6600 quad core CPU plus 3G DDR2 800M memory. Although I don't have good hard drives, marked only 5.1 in Windows 7 32 bit, I think in this test of the calculation of the summation of squares, the access to hard drives might not be significant. The graphic card used is a GeForce 9800 GTX+ with 512M GDDR3 memory. The card is shown as


Algorithm in raw CUDA

The test case I used is solving the summation of squares of an array of integers (random numbers ranged from 0 to 9), and, as I mentioned, a GeForce 9800 GTX+ graphic card running within Windows 7 32-bit system was employed for the testing. If in plain C language, the summation could be implemented by the following loop code, which is then executed on a CPU core:

int final_sum = 0;
for (int i = 0; i < DATA_SIZE; i++) {
    final_sum += data[i] * data[i];
}
Obviously, it is a serial computation. The code is executed in a serial stream of instructions. In order to utilise the power of CUDA, the algorithm has to be parallelised, and the more parallelisation are realised, the more potential power will be explored. With the help of my basic understanding on CUDA, I split the data into different groups and then used the equivalent number of threads on the GPU to calculate the summation of the squares of each group. Ultimately results from all the groups are added together to obtain the final result.

The algorithm designed is briefly shown in the figure


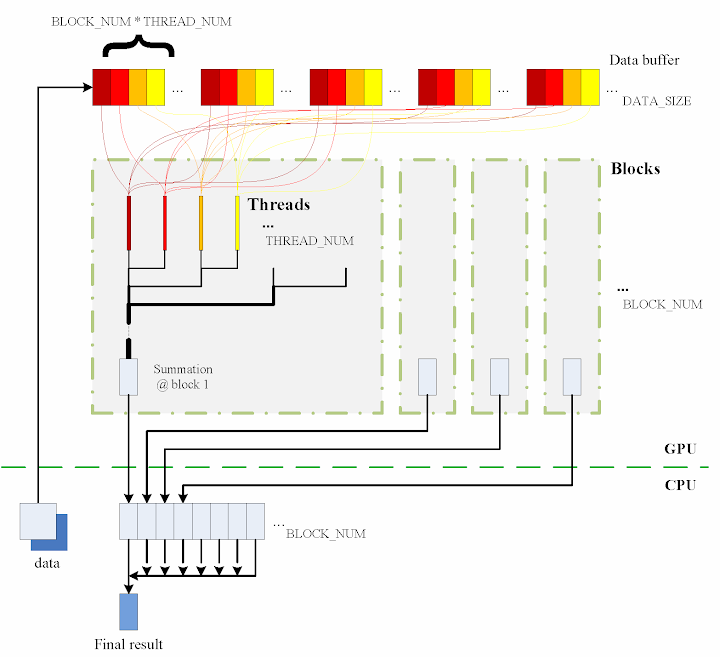
The consecutive steps are:

1. Copy data from the CPU memory to the GPU memory.

cudaMemcpy(gpudata, data, sizeof(int) * DATA_SIZE, cudaMemcpyHostToDevice);

2. Totally BLOCK_NUM blocks are used, and in each block THREAD_NUM threads are produced to perform the calculation. In practice, I used THREAD_NUM = 512, which is the greatest allowed thread number in a block of CUDA. Thereby, the raw data are seperated into DATA_SIZE / (BLOCK_NUM * THREAD_NUM) groups.

3. The access to the data buffer is designed as consecutive, otherwise the efficiency will be reduced.

4. Each thread does its corresponding calculation.

shared[tid] = 0;
for (int i = bid * THREAD_NUM + tid; i < DATA_SIZE; i += BLOCK_NUM * THREAD_NUM) {
    shared[tid] += num[i] * num[i];
}

5. By using shared memory in the blocks, sub summation can be done in each block. Also, the sub summation is parallelised to achieve as high execution speed as possible. Please refer to the source code regarding the details of this part.

6. The BLOCK_NUM sub summation results for all the blocks are copied back to the CPU side, and they are then added together to obtain the final value

cudaMemcpy(&sum, result, sizeof(int) * BLOCK_NUM, cudaMemcpyDeviceToHost);

int final_sum = 0;
for (int i = 0; i < BLOCK_NUM; i++) {
    final_sum += sum[i];
}

Regarding the procedure, function QueryPerformanceCounter records the code execution duration, which is then used for comparison between the different implementations. Before each call of QueryPerformanceCounter, CUDA function cudaThreadSynchronize() is called to make sure that all computations on the GPU are really finished. (Please refer to the CUDA Best Practices Guide §2.1.)

Algorithm in thrust

The application of the library thrust could make the CUDA code as simple as a plain C++ one. The usage of the library is also compatible with the usage of STL (Standard Template Library) of C++. For instance, the code for the calculation on GPU utilising thrust support is scratched like this:

thrust::host_vector<int> data(DATA_SIZE);
srand(time(NULL));
thrust::generate(data.begin(), data.end(), random());

cudaThreadSynchronize();
QueryPerformanceCounter(&elapsed_time_start);

thrust::device_vector<int> gpudata = data;

int final_sum = thrust::transform_reduce(gpudata.begin(), gpudata.end(),
    square<int>(), 0, thrust::plus<int>());

cudaThreadSynchronize();
QueryPerformanceCounter(&elapsed_time_end);
elapsed_time = (double)(elapsed_time_end.QuadPart - elapsed_time_start.QuadPart)
    / frequency.QuadPart;

printf("sum (on GPU): %d; time: %lf\n", final_sum, elapsed_time);

thrust::generate is used to generate the random data, for which the functor random is defined in advance. random was customised to generate a random integer ranged from 0 to 9.

// define functor for
// random number ranged in [0, 9]
class random
{
public:
    int operator() ()
    {
        return rand() % 10;
    }
};

In comparison with the random number generation without thrust, the code could however not be as elegant.

// generate random number ranged in [0, 9]
void GenerateNumbers(int * number, int size)
{
    srand(time(NULL));
    for (int i = 0; i < size; i++) {
        number[i] = rand() % 10;
    }
}

Similarly square is a transformation functor taking one argument. Please refer to the source code for its definition. square was defined for __host__ __device__ and thus it can be used for both the CPU and the GPU sides.

// define transformation f(x) -> x^2
template <typename T>
struct square
{
    __host__ __device__
        T operator() (T x)
    {
        return x * x;
    }
};

That is all for the thrust based code. Is it concise enough? :) Here function QueryPerformanceCounter also records the code duration. On the other hand, the host_vector data is operated on CPU to compare. Using the code below, the summation is performed by the CPU end:

QueryPerformanceCounter(&elapsed_time_start);

final_sum = thrust::transform_reduce(data.begin(), data.end(),
    square<int>(), 0, thrust::plus<int>());

QueryPerformanceCounter(&elapsed_time_end);
elapsed_time = (double)(elapsed_time_end.QuadPart - elapsed_time_start.QuadPart)
    / frequency.QuadPart;

printf("sum (on CPU): %d; time: %lf\n", final_sum, elapsed_time);

I also tested the performance if use thrust::host_vector<int> data as a plain array. This is supposed to cost more overhead, I thought, but we might be curious to know how much. The corresponding code is listed as

final_sum = 0;
for (int i = 0; i < DATA_SIZE; i++)
{
    final_sum += data[i] * data[i];
}

printf("sum (on CPU): %d; time: %lf\n", final_sum, elapsed_time);

The execution time was recorded to compare as well.

Test results on GPU & CPU

The previous experiences show that GPU surpasses CPU when massive parallel computation is realised. When DATA_SIZE increases, the potential of GPU calculation will be gradually released. This is predictable. Moreover, do we lose efficiency when we apply thrust? I guess so, since there is extra cost brought, but do we lose much? We have to judge from the comparison results.

When DATA_SIZE increases from 1 M to 32 M (1 M equals to 1 * 1024 * 1024), the results obtained are illustrated as the table


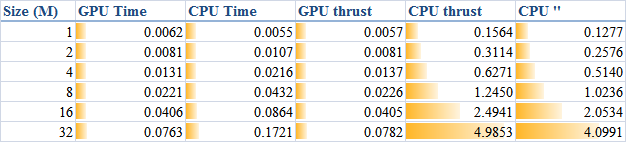
The descriptions of the items are:

• GPU Time: execution time of the raw CUDA code;
• CPU Time: execution time of the plain loop code running on the CPU;
• GPU thrust: execution time of the CUDA code with thrust;
• CPU thrust: execution time of the CPU code with thrust;
• CPU '': execution time of the plain loop code based on thrust::
  host_vector.

The corresponding trends can be summarised as


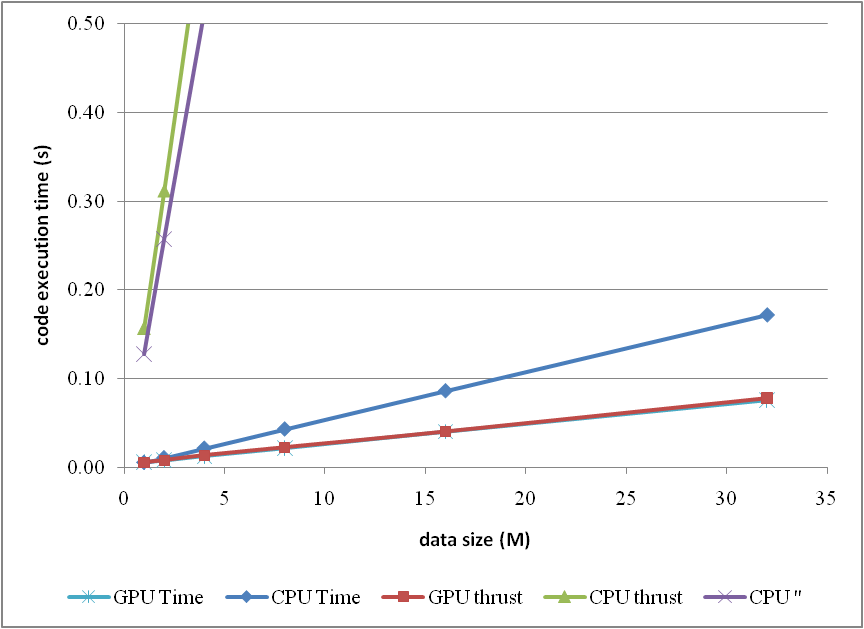
or compare them by the column figure


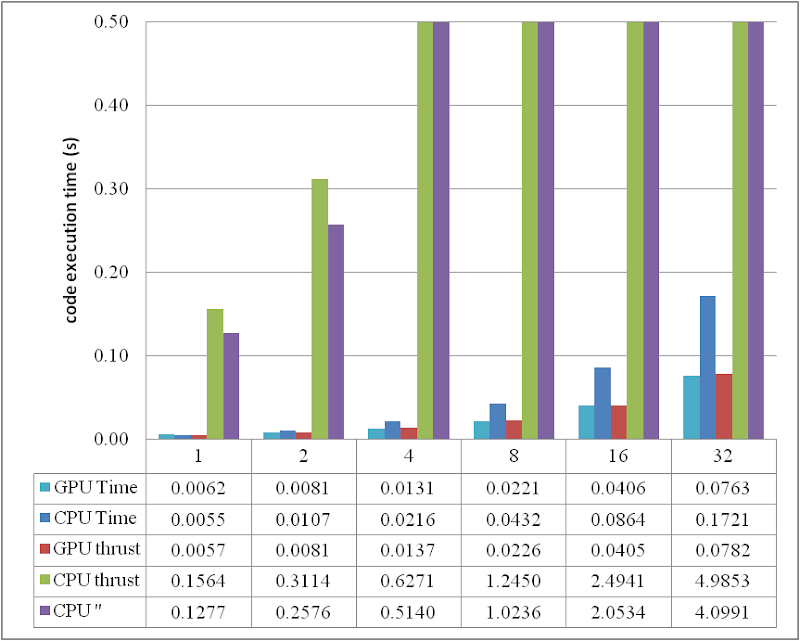
The speedup of GPU to CPU is obvious when DATA_SIZE is more than 4 M. Actually with greater data size, much better performance speedup can be obtained. Interestingly, in this region, the cost of using thrust is quite small, which can even be neglected. However, on the other hand, don't use thrust on the CPU side, neither thrust::transform_reduce method nor a plain loop on a thrust::host_vector; according to the figures, the cost brought is huge. Use a plain array and a loop instead.

From the comparison figure, we found that the application of thrust not only simplifies the code of CUDA computation, but also compensates the loss of efficiency when DATA_SIZE is relatively small. Therefore, it is strongly recommended.

Conclusion

Based on the tests performed, apparently, by employing parallelism, GPU shows greater potential than CPU does, especially for those calculations which contains much more parallel elements. This article also found that the application of thrust does not reduce the code execution efficiency on the GPU side, but brings dramatical negtive changes in the efficiency on the CPU side. Consequently, it is better using plain arrays for CPU calculations.

In conclusion, the usage of thrust feels pretty good, because it improves the code efficiency, and with employing thrust, the CUDA code can be so concise and rapidly developed.

ps - This post can also be referred from one of my articles published on CodeProject, "A brief test on the code efficiency of CUDA and thrust", which could be more complete and source code is attached as well. Any comments are sincerely welcome.

Additionally, the code was built and tested in Windows 7 32 bit plus Visual Studio 2008, CUDA 3.0 and the latest thrust 1.2. One also needs a NVIDIA graphic card as well as CUDA toolkit to run the programs. For instructions on installing CUDA, please refer to its official site CUDA Zone.